2022年6月27日至7月9日，皇冠9393体育平台举办的暑期国际讲堂《李代数与可积双曲方程》通过腾讯会议APP圆满完成授课。该课程由莫斯科国立大学教授Dmitry V Millionshchikov（Millionshchikov是代数拓扑学及其应用、微分几何和幂零李代数理论及其应用等领域的知名专家。他还是莫斯科国立大学罗蒙诺索夫分校高等几何学和拓扑学系的副主任）和Sergey V. Smirnov（Smirnov曾多次在北京大学，密歇根州立大学，莫斯科独立大学做讲座）讲授。来自数学、机电及伦敦玛丽女王等学院的本科生、博士生及旁听生参加了该课程。

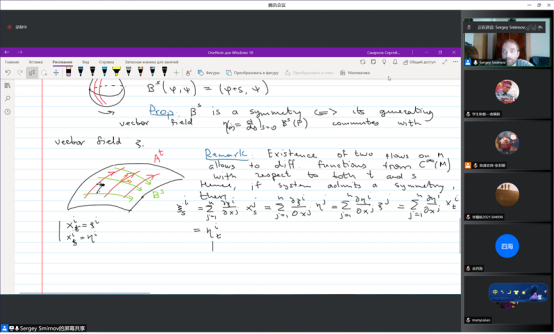
       课程采取两位教授轮流讲授的方式，首先，Smirnov教授介绍了可积性和流形的概念，将微分流形的辛结构联系于向量空间的辛结构，并以此为基础讨论了各类常微分方程和偏微分方程的可积性。尤其是双曲型偏微分方程，Smirnov教授指出对于波动方程而言，其象征的水平集为双曲面。

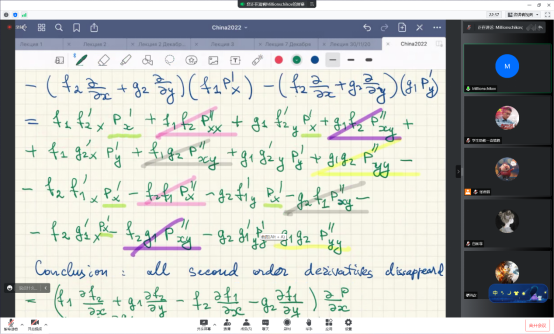
       其次，Millionshchikov教授强调了李代数在可积系统理论中的重要作用。他介绍了李代数的概念，带领学生研究李代数的一些基本性质，并考虑重要示例。

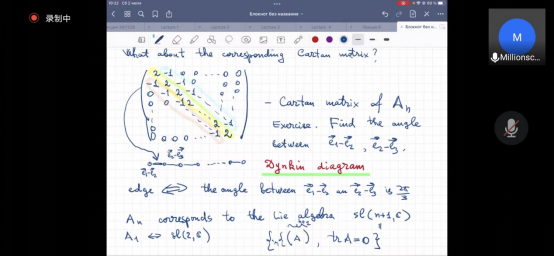
       同时他介绍可用于研究可积双曲方程的一个重要工具——特征代数的概念，描述了与经典简单李代数的Cartan矩阵对应的二维Todalatic的特征代数（这些系统推广了双曲Liouville方程）和与仿射李代数的退化Cartan矩阵相关的指数系统（特别是推广了众所周知的sine-gordon方程）。

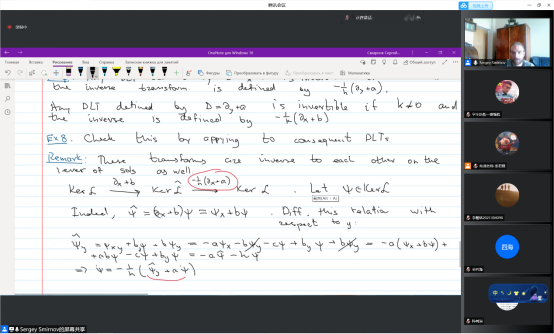
       最后，Smirnov教授讨论了这些代数的增长性质及其与相应指数系统的更高对称性的关系以及这些可积双曲奇异值系统的离散类似物。

       两位教授讲课旁征博引，深入浅出，使学生对李代数与可积双曲方程中的经典问题和方法有了基本的认识。授课期间采取传统板书方式，结合图示，方便学生更好地理解课程中的问题和方法。通过对本门课程的学习，学生们对李代数与可积双曲方程中的基本问题和研究方法都有了清晰的认识，收获颇丰。

       团队负责人肖曼玉老师就本次课程的圆满成功进行了总结和回顾。她向两位教授的辛苦授课表示了衷心的感谢，也对坚持下来的学生给予了鼓励。期待他们下次更精彩的课堂。

       授课期间，Smirnov教授和Millionshchikov教授通过电子邮件及时发送教学手稿，助课老师张君丽录制教学视频并整理手稿，保证大家能够提前预习、及时复习，极大地提高了学生的学习积极性。课程结束后，得到了学生热情的感谢和积极的反馈，为明年再次举办暑期课堂提供了宝贵的经验。

图文：张君丽  袁镜程

审核：都琳